35. Inventory Dynamics#
35.1. Overview#
In this lecture, we will study the time path of inventories for firms that follow so-called s-S inventory dynamics.
Such firms
wait until inventory falls below some level \(s\) and then
order sufficient quantities to bring their inventory back up to capacity \(S\).
These kinds of policies are common in practice and are also optimal in certain circumstances.
A review of early literature and some macroeconomic implications can be found in [Caplin, 1985].
Here, our main aim is to learn more about simulation, time series, and Markov dynamics.
While our Markov environment and many of the concepts we consider are related to those found in our lecture Finite Markov Chains, the state space is a continuum in the current application.
Let’s start with some imports
from typing import NamedTuple
import jax
import jax.numpy as jnp
from jax import random
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
Matplotlib is building the font cache; this may take a moment.
35.2. Sample paths#
Consider a firm with inventory \(X_t\).
The firm waits until \(X_t \leq s\) and then restocks up to \(S\) units.
It faces stochastic demand \(\{ D_t \}\), which we assume is IID.
With notation \(a^+ := \max\{a, 0\}\), inventory dynamics can be written as
In what follows, we will assume that each \(D_t\) is lognormal, so that
where \(\mu\) and \(\sigma\) are parameters and \(\{Z_t\}\) is IID and standard normal.
Here’s a class that stores parameters and generates time paths for inventory.
class Firm(NamedTuple):
s: int # restock trigger level
S: int # capacity
μ: float # shock location parameter
σ: float # shock scale parameter
@jax.jit
def sim_inventory_path(firm, x_init, random_keys):
"""
Simulate inventory path.
Args:
firm: Firm object
x_init: Initial inventory level
random_keys: Array of JAX random keys of length sim_length - 1.
Returns:
Array of inventory levels over time
"""
def update_step(carry, key_t):
"""
Single update step
"""
x = carry
Z = random.normal(key_t)
D = jnp.exp(firm.μ + firm.σ * Z)
new_x = jax.lax.cond(
x <= firm.s,
lambda: jnp.maximum(
firm.S - D, 0.0
), # Reorder to S, then subtract demand
lambda: jnp.maximum(x - D, 0.0), # Just subtract demand
)
return new_x, new_x
# Use scan to iterate through time steps
final_x, X_path = jax.lax.scan(update_step, x_init, random_keys)
# Prepend initial value
X = jnp.concatenate([jnp.array([x_init]), X_path])
return X
firm = Firm(s=10, S=100, μ=1.0, σ=0.5)
sim_length = 100
x_init = 50
# Generate `sim_length-1` keys as `x_init` will be first array element
keys = random.split(random.PRNGKey(21), sim_length - 1)
X = sim_inventory_path(firm, x_init, keys)
Let’s run a first simulation, of a single path:
s, S = firm.s, firm.S
fig, ax = plt.subplots()
bbox = (0.0, 1.02, 1.0, 0.102)
legend_args = {"ncol": 3, "bbox_to_anchor": bbox, "loc": 3, "mode": "expand"}
ax.plot(X, label="inventory")
ax.plot(jnp.full(sim_length, s), "k--", label="$s$")
ax.plot(jnp.full(sim_length, S), "k-", label="$S$")
ax.set_ylim(0, S + 10)
ax.set_xlabel("time")
ax.legend(**legend_args)
plt.show()
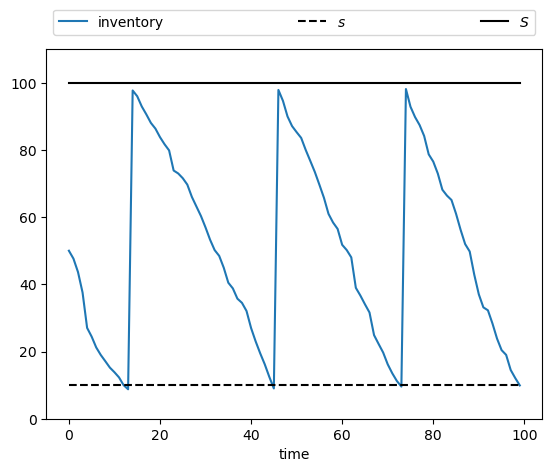
Now let’s simulate multiple paths in order to build a more complete picture of the probabilities of different outcomes:
sim_length = 200
fig, ax = plt.subplots()
ax.plot(jnp.full(sim_length, s), "k--", label="$s$")
ax.plot(jnp.full(sim_length, S), "k-", label="$S$")
ax.set_ylim(0, S + 10)
ax.legend(**legend_args)
for i in range(400):
# Generate `sim_length-1` keys as `x_init` will be first array element
keys = random.split(random.PRNGKey(i), sim_length - 1)
X = sim_inventory_path(firm, x_init, keys)
ax.plot(X, "b", alpha=0.2, lw=0.5)
plt.show()
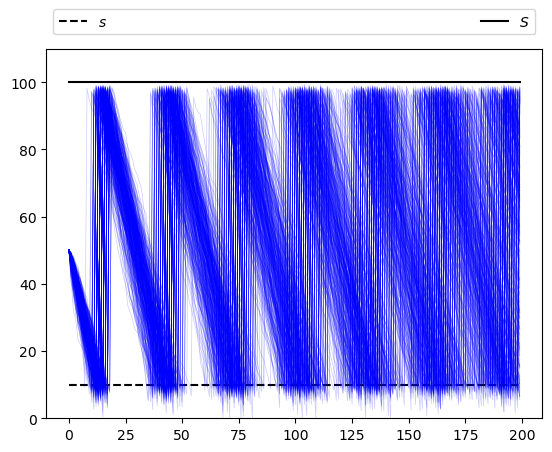
35.3. Marginal distributions#
Now let’s look at the marginal distribution \(\psi_T\) of \(X_T\) for some fixed \(T\).
We will do this by generating many draws of \(X_T\) given initial condition \(X_0\).
With these draws of \(X_T\) we can build up a picture of its distribution \(\psi_T\).
Here’s one visualization, with \(T=50\).
T = 50
M = 200 # Number of draws
ymin, ymax = 0, S + 10
fig, axes = plt.subplots(1, 2, figsize=(11, 6))
for ax in axes:
ax.grid(alpha=0.4)
ax = axes[0]
ax.set_ylim(ymin, ymax)
ax.set_ylabel("$X_t$", fontsize=16)
ax.vlines((T,), -1.5, 1.5)
ax.set_xticks((T,))
ax.set_xticklabels((r"$T$",))
sample = []
for m in range(M):
keys = random.split(random.PRNGKey(m), sim_length - 1)
X = sim_inventory_path(firm, x_init, keys)
ax.plot(X, "b-", lw=1, alpha=0.5)
ax.plot((T,), (X[T+1],), "ko", alpha=0.5)
sample.append(X[T+1])
axes[1].set_ylim(ymin, ymax)
axes[1].hist(
sample,
bins=16,
density=True,
orientation="horizontal",
histtype="bar",
alpha=0.5,
)
plt.show()
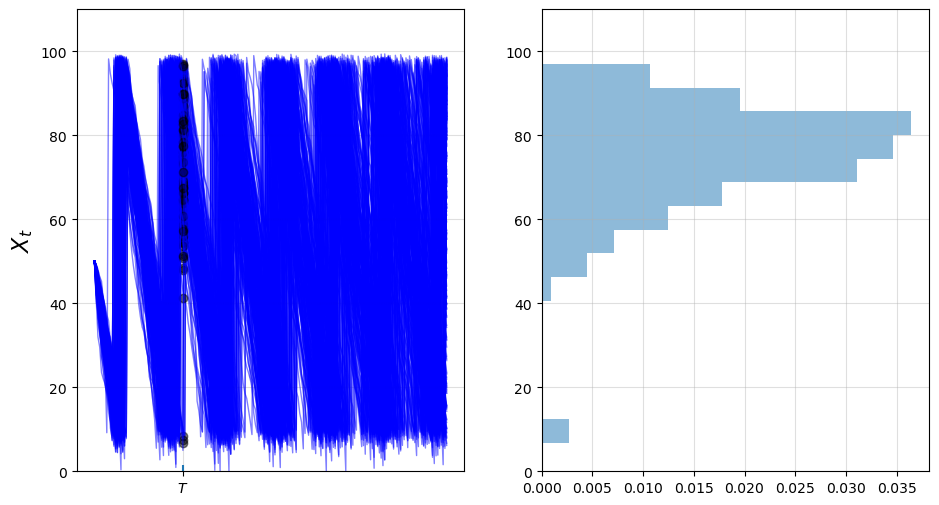
We can build up a clearer picture by drawing more samples
T = 50
M = 50_000
fig, ax = plt.subplots()
sample = []
for m in range(M):
keys = random.split(random.PRNGKey(m), T)
X = sim_inventory_path(firm, x_init, keys)
sample.append(X[T])
# Convert to JAX array
sample = jnp.array(sample)
ax.hist(sample, bins=36, density=True, histtype="bar", alpha=0.75)
plt.show()
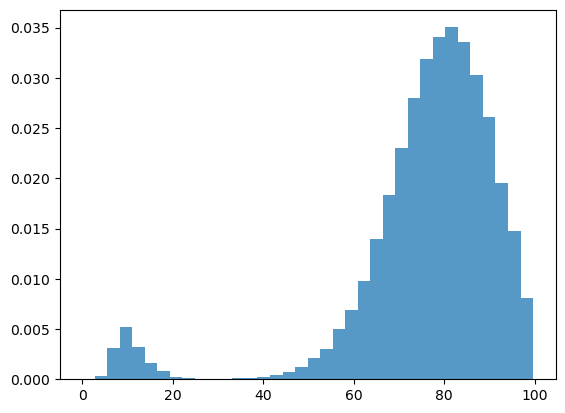
Note that the distribution is bimodal
Most firms have restocked twice but a few have restocked only once (see figure with paths above).
Firms in the second category have lower inventory.
We can also approximate the distribution using a kernel density estimator.
Kernel density estimators can be thought of as smoothed histograms.
They are preferable to histograms when the distribution being estimated is likely to be smooth.
We will use a kernel density estimator from scikit-learn
def plot_kde(sample, ax, label=""):
xmin, xmax = 0.9 * min(sample), 1.1 * max(sample)
xgrid = jnp.linspace(xmin, xmax, 200)
kde = KernelDensity(kernel="gaussian").fit(sample[:, None])
log_dens = kde.score_samples(xgrid[:, None])
ax.plot(xgrid, jnp.exp(log_dens), label=label)
fig, ax = plt.subplots()
plot_kde(sample, ax)
plt.show()
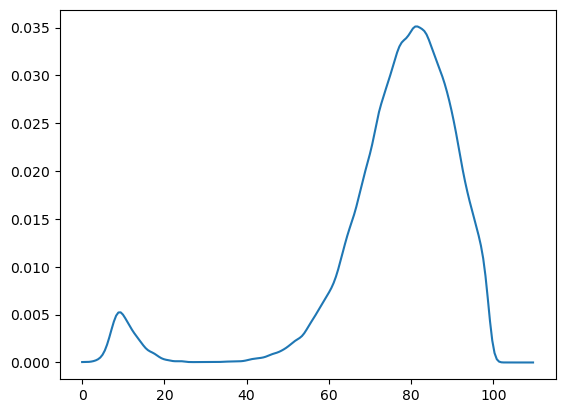
The allocation of probability mass is similar to what was shown by the histogram just above.
35.4. Exercises#
Exercise 35.1
This model is asymptotically stationary, with a unique stationary distribution.
(See the discussion of stationarity in our lecture on AR(1) processes for background — the fundamental concepts are the same.)
In particular, the sequence of marginal distributions \(\{\psi_t\}\) is converging to a unique limiting distribution that does not depend on initial conditions.
Although we will not prove this here, we can investigate it using simulation.
Your task is to generate and plot the sequence \(\{\psi_t\}\) at times \(t = 10, 50, 250, 500, 750\) based on the discussion above.
(The kernel density estimator is probably the best way to present each distribution.)
You should see convergence, in the sense that differences between successive distributions are getting smaller.
Try different initial conditions to verify that, in the long run, the distribution is invariant across initial conditions.
Solution to Exercise 35.1
Below is one possible solution:
The computations involve a lot of CPU cycles so we have tried to write the
code efficiently using jax.jit and jax.vmap to run on CPU/GPU.
@jax.jit
def simulate_single_firm(x_init, period_keys):
"""
Simulate a single firm forward by num_periods.
Args:
x_init: Initial inventory level for this firm
period_keys: Random key for this firm for each period
"""
def update_step(x, period_key):
Z = random.normal(period_key)
D = jnp.exp(firm.μ + firm.σ * Z)
new_x = jax.lax.cond(
x <= firm.s,
lambda: jnp.maximum(firm.S - D, 0.0),
lambda: jnp.maximum(x - D, 0.0),
)
return (
new_x,
None,
) # Return None for scan accumulator (we don't need it)
# Simulate forward num_periods
final_x, _ = jax.lax.scan(update_step, x_init, period_keys)
return final_x
# Vectorize over all firms using vmap
vectorized_simulate = jax.vmap(simulate_single_firm, in_axes=(0, 0))
def shift_firms_forward(firm, current_inventory_levels, num_periods, key):
"""
Shift multiple firms forward by num_periods using JAX vectorization.
Returns:
Array of new inventory levels after num_periods
"""
# Generate independent random keys for each firm
num_firms = len(current_inventory_levels)
firm_keys = random.split(key, (num_firms, num_periods))
# Run simulation for all firms in parallel
new_inventory_levels = vectorized_simulate(
current_inventory_levels, firm_keys
)
return new_inventory_levels
x_init = 50
num_firms = 50_000
sample_dates = 0, 10, 50, 250, 500, 750
first_diffs = jnp.diff(jnp.array(sample_dates))
fig, ax = plt.subplots()
X = jnp.full(num_firms, x_init)
current_date = 0
for d in first_diffs:
X = shift_firms_forward(firm, X, d, random.PRNGKey(current_date + 1))
current_date += d
plot_kde(X, ax, label=f"t = {current_date}")
ax.set_xlabel("inventory")
ax.set_ylabel("probability")
ax.legend()
plt.show()
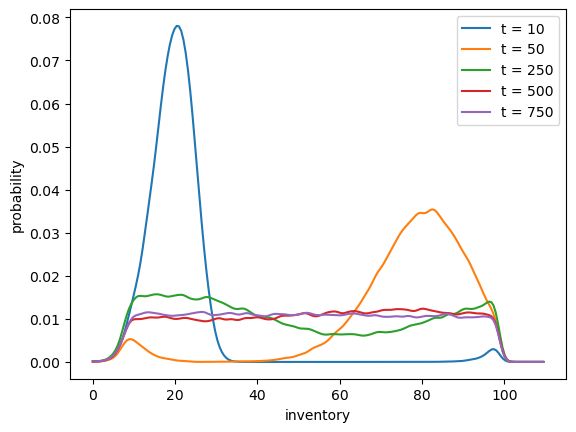
Notice that by \(t=500\) or \(t=750\) the densities are barely changing.
We have reached a reasonable approximation of the stationary density.
You can convince yourself that initial conditions don’t matter by testing a few of them.
For example, try rerunning the code above with all firms starting at \(X_0 = 20\) or \(X_0 = 80\).
Exercise 35.2
Using simulation, calculate the probability that firms that start with \(X_0 = 70\) need to order twice or more in the first 50 periods.
You will need a large sample size to get an accurate reading.
Solution to Exercise 35.2
Here is one solution.
Again, the computations are relatively intensive so we have written a
specialized JAX-jitted function and using jax.vmap to use parallelization across firms.
Note the time the routine takes to run, as well as the output.
@jax.jit
def simulate_single_firm(period_keys):
"""
Simulate a single firm and count restocks.
Args:
period_keys: Random key for all the periods
Returns:
1 if firm restocks > 1 times, 0 otherwise
"""
def update_step(carry, period_key):
x, restock_count = carry
Z = random.normal(period_key)
D = jnp.exp(firm.μ + firm.σ * Z)
# Check if we need to restock and update accordingly
def restock_branch():
new_x = jnp.maximum(firm.S - D, 0.0)
new_restock_count = restock_count + 1
return (new_x, new_restock_count)
def no_restock_branch():
new_x = jnp.maximum(x - D, 0.0)
return (new_x, restock_count)
new_carry = jax.lax.cond(
x <= firm.s, restock_branch, no_restock_branch
)
return new_carry, None
# Initial state: (inventory_level, restock_count)
initial_carry = (x_init, 0)
# Simulate through all periods
(final_x, total_restocks), _ = jax.lax.scan(
update_step, initial_carry, period_keys
)
# Return 1 if restocked more than once, 0 otherwise
return jnp.where(total_restocks > 1, 1, 0)
# Vectorize the simulation across all firms
vectorized_simulate = jax.vmap(simulate_single_firm, in_axes=(0,))
def compute_freq(
firm, sim_length=50, x_init=70, num_firms=1_000_000, key=random.PRNGKey(2)
):
"""
Compute the frequency of firms that restock 2 or more times using JAX.
Args:
firm: Firm dataclass
sim_length: Length of simulation for each firm
x_init: Initial inventory level for all firms
num_firms: Number of firms to simulate
key: JAX random key
Returns:
Fraction of firms that restock 2 or more times
"""
# Generate independent random keys for each firm
firm_keys = random.split(key, (num_firms, sim_length))
# Run simulation for all firms
restock_indicators = vectorized_simulate(firm_keys)
# Compute frequency (fraction of firms that restocked > 1 times)
frequency = jnp.mean(restock_indicators)
return frequency
%%time
freq = compute_freq(firm)
print(f"Frequency of at least two stock outs = {freq}")
Frequency of at least two stock outs = 0.9599350094795227
CPU times: user 756 ms, sys: 20.5 ms, total: 777 ms
Wall time: 750 ms